If you haven't heard of them, Yasso 800s comprise a infamous running workout that touts itself to predict your marathon time. The name was coined by Amby Burfoot, paying homage to Runner's World editor Bart Yasso.
While even Yasso himself has professed he had no idea why the math worked, many others have remained stumped. No more! First, let's define the workout:
- Run 10 800-meter intervals, with 2–3 minutes rest.
- Take you average time for the intervals, replace the minutes with hours, the seconds with minutes, and that’s your marathon time!
If you ran the repeats averaging 3:35 (minutes:seconds), that means you’re ready to run 3:35 (hours:minutes) in the marathon. Simple.
The trick here is also simple: you’re multiplying your time by 60, but the distance by only 52.4 (.5 miles to 26.2 miles), so the pace is slower. Note that you have done 10 repeats so the pace of the repeats themselves is closer to what you can run for 5 miles. Let your time for the repeats by t₁, and the time for the marathon t₂. Yasso says that t₂ = 60 ⋅ t₁. So in the same amount of time, you cover less distance. In doing so, we’re saying you pace will only be 52.4/60 = 87.3% of your pace on intervals, so you’re running 87.3% of the pace you can for about 5 miles.
That helped, right? Almost! Thanks to work done by academic studies, we know that the pace/distance curve has another neat, mathematical property: it follows a power law. The power law curve is so-named because it resembles y = axᵇ , where x is raised to the b-th power.
Let’s check this formula ourselves
To understand this relationship, take a look at the record times at distances ranging from the 100 meters through the marathon. While no single athlete would be ready for events from the 100m through the marathon, we can consider the best times in event as a measure of what is possible. World record performances are here on Wikipedia, and we convert to CSV using this webpage. We end up with data like this:
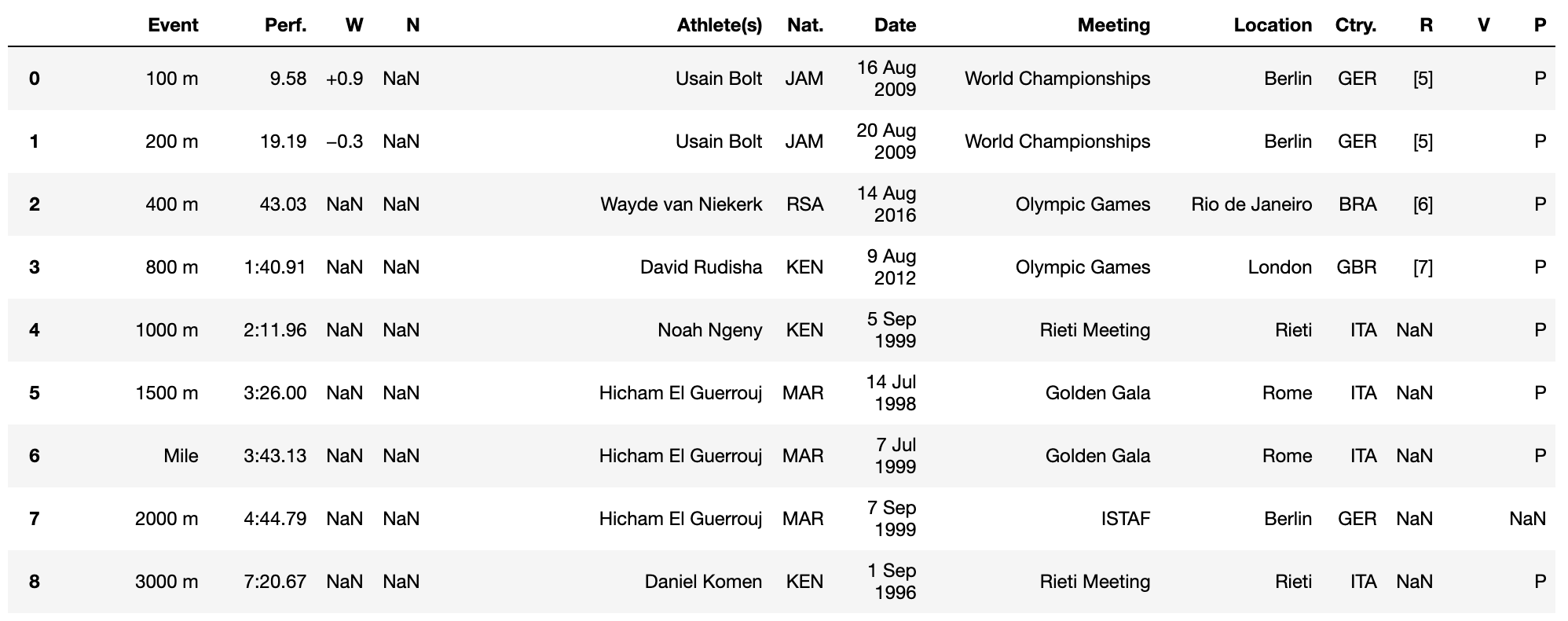
To understand the data, we’ll start by making a plot of pace vs distance.
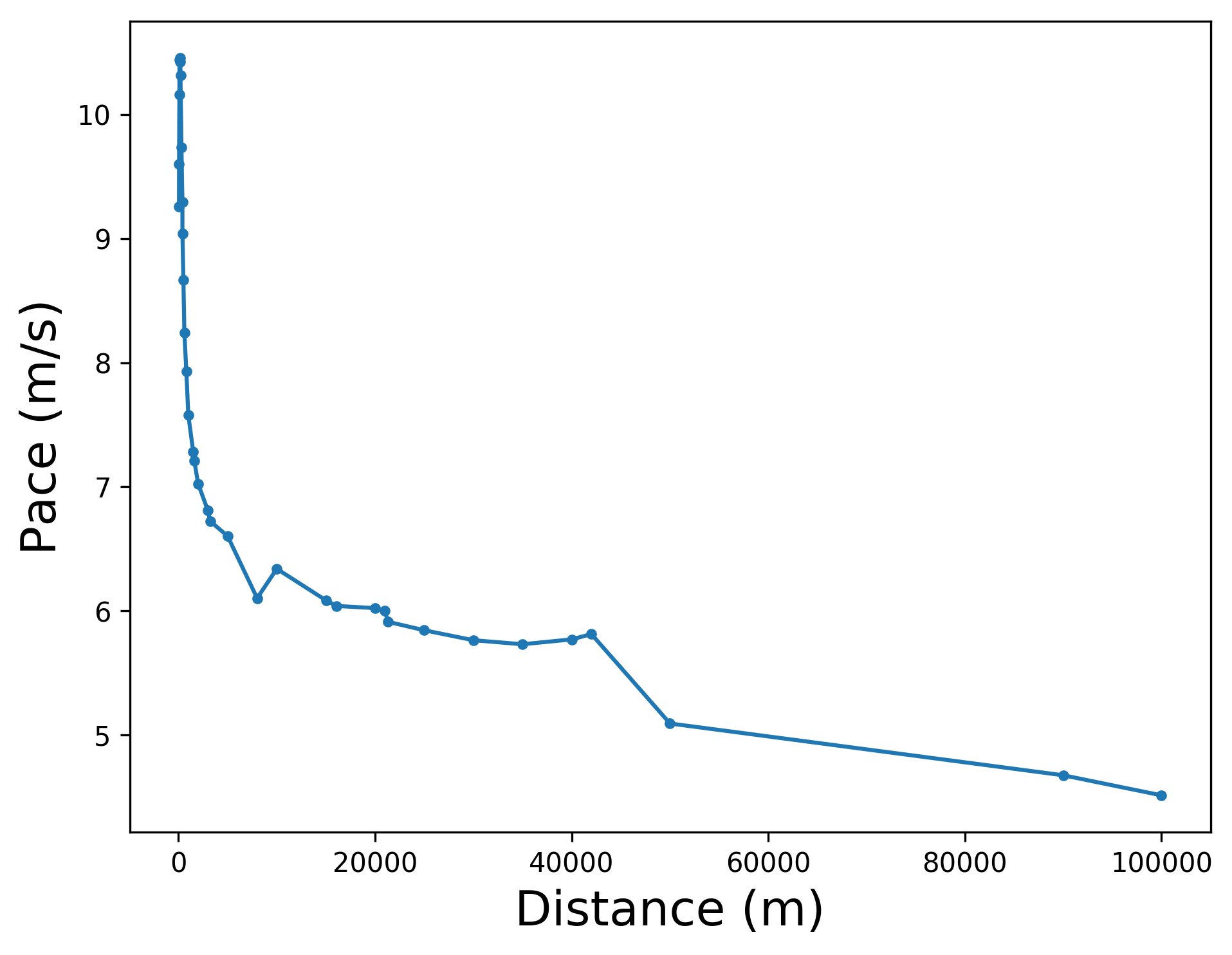
While that curve doesn’t look special to most, to those familiar with Complex Systems see that it has the makings of a power law. As we mentioned, analysis has already been done to show that the a power law model will fit this data, and let’s take a look for ourselves. The first thing we need to is plot this data in log-log space.
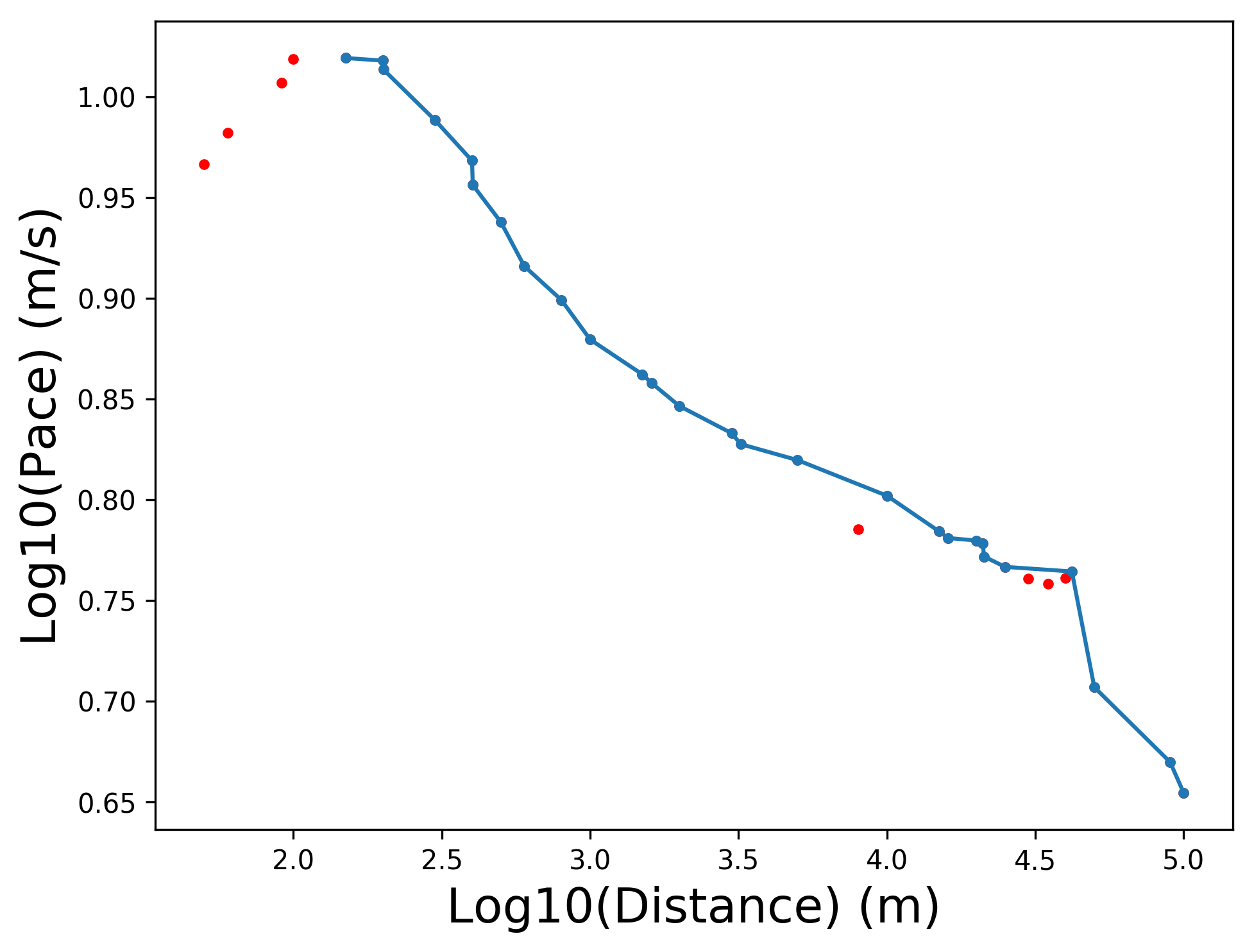
Hey, it (sortof) looks like a straight line now! Now we can fit a simple regression line to the data, and that will give us the coefficients on the power law model. The regression in log space gives us a fit show on the next plot. I’ve excluded the points in red that are slower than longer events.
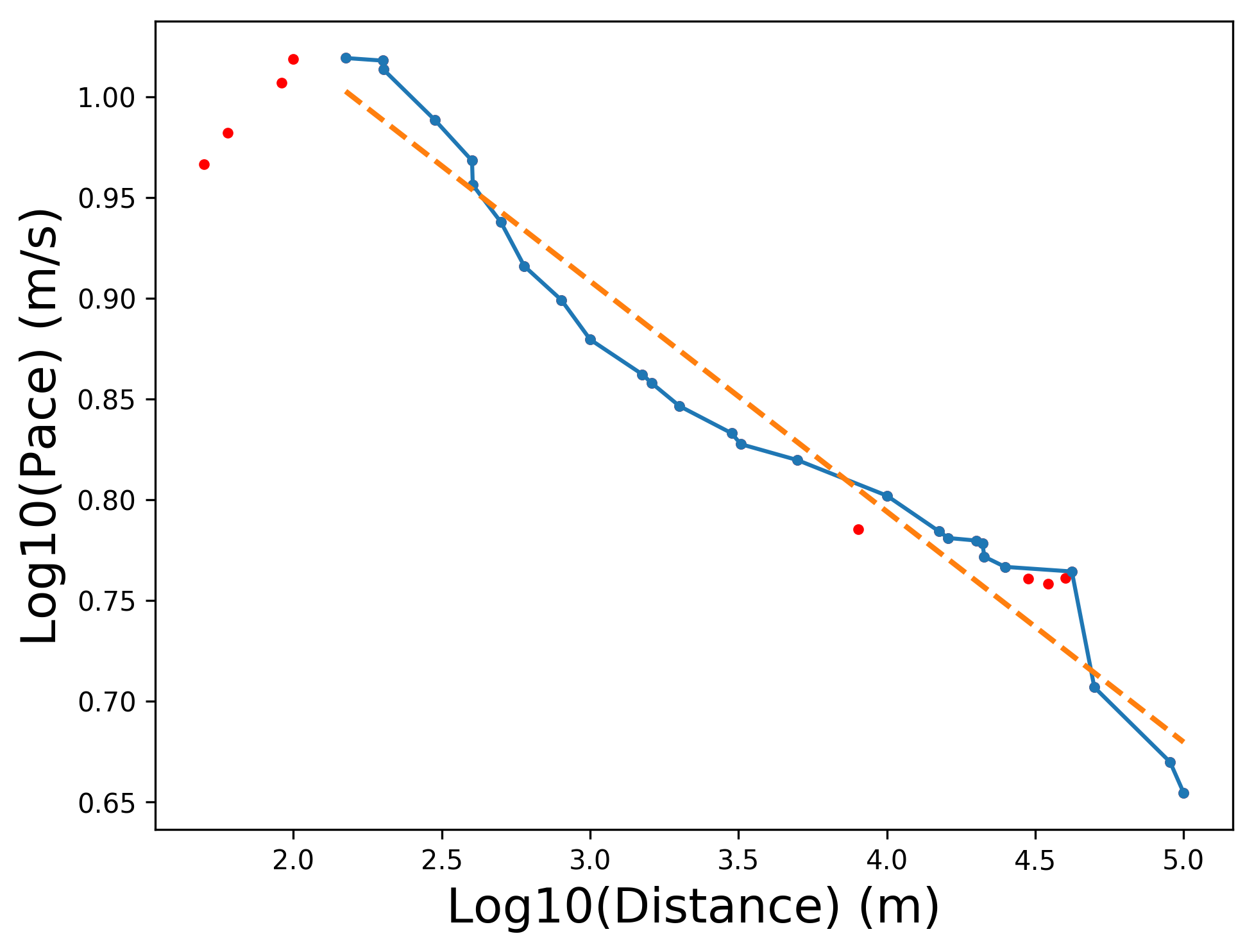
We found coefficients for pace = 17.85 ⋅ distance^(−0.1144).
Now let’s check Yasso’s math.
Earlier, we figured out that Yasso said marathon pace is 87% of your 800m pace (that you can repeat 10 times). As it turned out, that was the same as just multiplying the time by 60. For ourselves, we found a formula that gives us pace = 17.85 ⋅ distance^(−0.1144), based on the data, and that gives us a ratio of 82% from 5 miles to the marathon. So Yasso 800s are going to largely overestimate your pace for the marathon, if you’re running world record pace for both the 5mi and the marathon. If we compare our model to those fit on individual athletes, we do see that ours is “steeper”, such that it might be closer to 87% than 82%.
For fun, we can play around with these formulas to make new workouts! Next time you’re curious about your marathon potential,
- Go run 4 x mile.
- Take your mile split in seconds, multiply by 0.5, and that’s your marathon time in minutes!†
I’ll let you decide what to call this workout.
Footnotes
† Based on the formula we found, it should really be .55!